
M.Sc. Walter Otoniel Campos Granados
Investigador asociado Centro de Modelaje Matemático “Carlos Castillo Chávez” UFG. Docente Escuela de Matemática, Facultad de Ciencias Naturales y Matemática, UES. Investigador CMM-UES.
Análisis temporal de muertes en El Salvador: Subregistros de muertes por COVID-19
- ,
- , COVID19, Disruptores
Se ha tenido a disposición los datos de causas de muerte desde 2015 hasta septiembre de 2020, solicitados al RNPN, y compartidos por LAB-DAT. Las bases de datos están por años: 2015 al 2019 completos, mientras que para el año 2020 se tienen los datos hasta el 30 de septiembre.
Cada observación de las bases de datos, consta de un caso de deceso, y entre las variables que la constituyen, está la variable “causa de defunción” la cual describe la causa del deceso, que pueden ser varias causas, en algunos casos.
A partir de dichas bases de datos se construyó la serie temporal mensual de la cantidad de muertes por mes, desde enero de 2015 hasta septiembre de 2020, tratando los cuatro casos siguientes: muerte por enfermedad renal, muerte por algún tipo de paro (cardiaco, cardiorrespiratorio, entre otros), muerte por cáncer, y finalmente se consideran las muertes por cualquier causa, excepto las provocadas por arma de fuego y/o accidentes de tránsito, causas que se consideran que han sufrido un deceso en el año 2020 debido a la cuarentena obligatoria que se impuso.
Análisis de muertes por causas renales
De las bases de datos se extraen todos los casos de muertes cuya causa sea enfermedades renales y se construye la serie mensual desde enero de 2015 hasta septiembre de 2020.
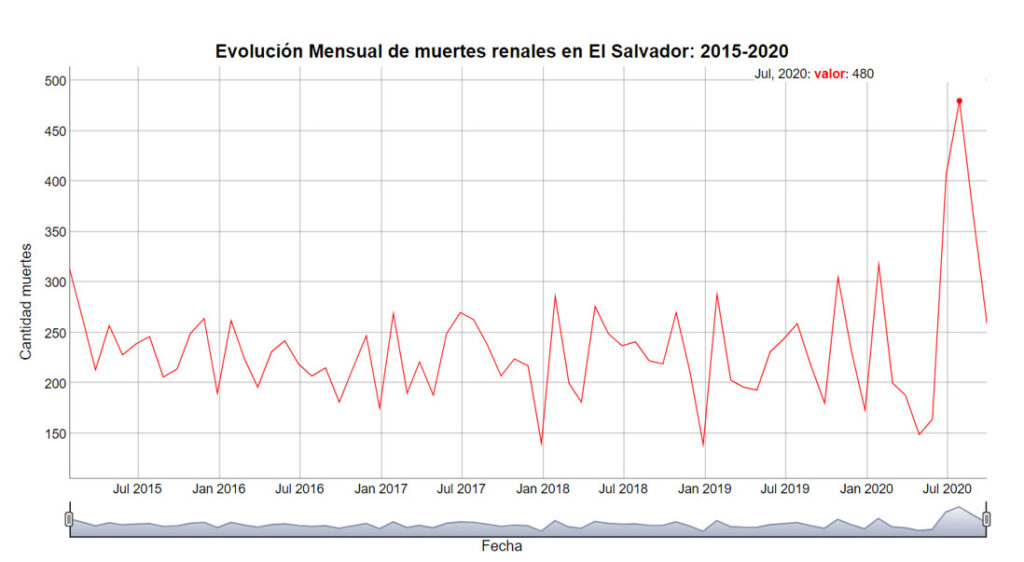
La Figura 1, muestra la evolución de muertes por causas renales, desde enero de 2015 hasta septiembre de 2020.
Figura 1.
Los datos desde 2015 hasta 2018 cumplen el test de Kolmogorov-Smirnov sobre la normalidad de los residuos, también desde 2015 hasta 2019 (p-valor de 0.97 y 0.72, respectivamente). Cuando se toman hasta septiembre de 2020 el p-valor baja hasta 0.32. En todos los casos los datos cumplen dicho test, lo cual permite poder construir modelos con métodos de series de tiempo, para predecir períodos a corto y mediano plazo, teniendo garantía que las predicciones serán robustas y altamente confiables.
La figura uno muestra la evolución de las muertes por causas renales, claramente se observa un cambio brusco de variabilidad en los datos correspondientes a los meses del año 2020.
Se trabaja el ajuste de los modelos utilizando la filosofía entrenamiento-prueba, de tal manera que se toman los datos mensuales desde 2015 hasta 2018 para entrenamiento del modelo y los datos mensuales del año 2019 para probar el modelo, tomando el que tenga menor error cuadrático medio entre las predicciones y los valores reales del año 2019.
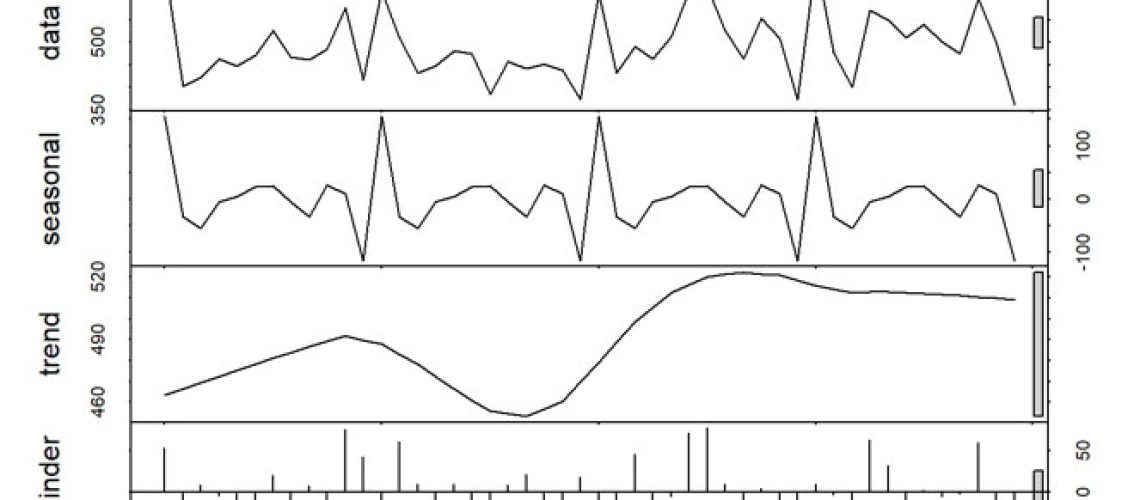
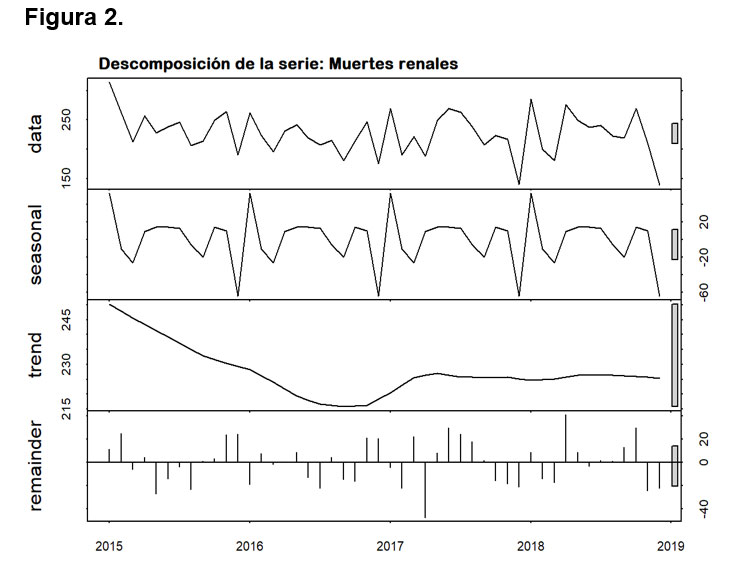
La figura 2, muestra la descomposición de la serie, se observa que no tiene tendencia los últimos años, una componente estacional anual y normalidad de los residuos.
Una vez que se han calibrado los modelos, se realizan las predicciones para los 12 meses del año 2020. Se realizan las predicciones y junto a ellas un intervalo de confianza con un nivel de confianza del 95%, por lo tanto, la probabilidad de que los datos reales estén en dicho intervalo de confianza es de 0.95.
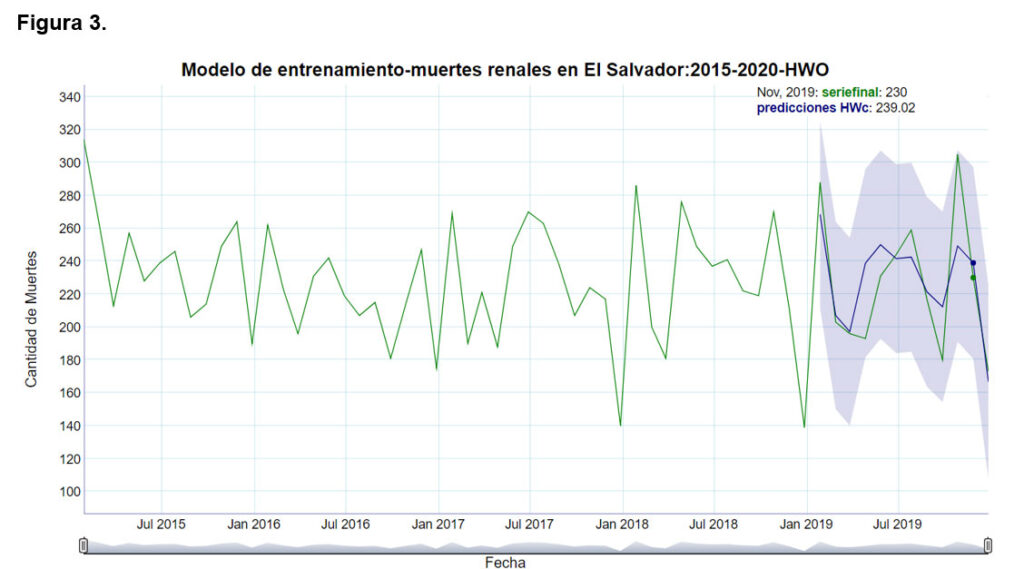
La figura tres muestra el modelo de entrenamiento con el método Holt-Winters, optimizado a través de una heurística personal desarrollada. Como anteriormente se señaló, con dicho modelo se realizan las predicciones para el año 2019 y se prueba su bondad de ajuste con los datos reales de dicho año, se toman los parámetros que minimizan el error cuadrático medio (eso es lo que hace el algoritmo desarrollado). Como se puede observar a nivel gráfico, el ajuste de las predicciones es excelente y el intervalo de confianza generado, sigue la tendencia de los datos reales, de acuerdo al periodo estacional anual de la serie. Para este modelo se obtiene un error cuadrático medio de 24.87
La figura cuatro muestra el nivel de ajuste del modelo de entrenamiento, utilizando el método de Box-Jenkins, el cual supone un modelo SARIMA (1,0,1)(0,1,1)[12].
Figura 4.
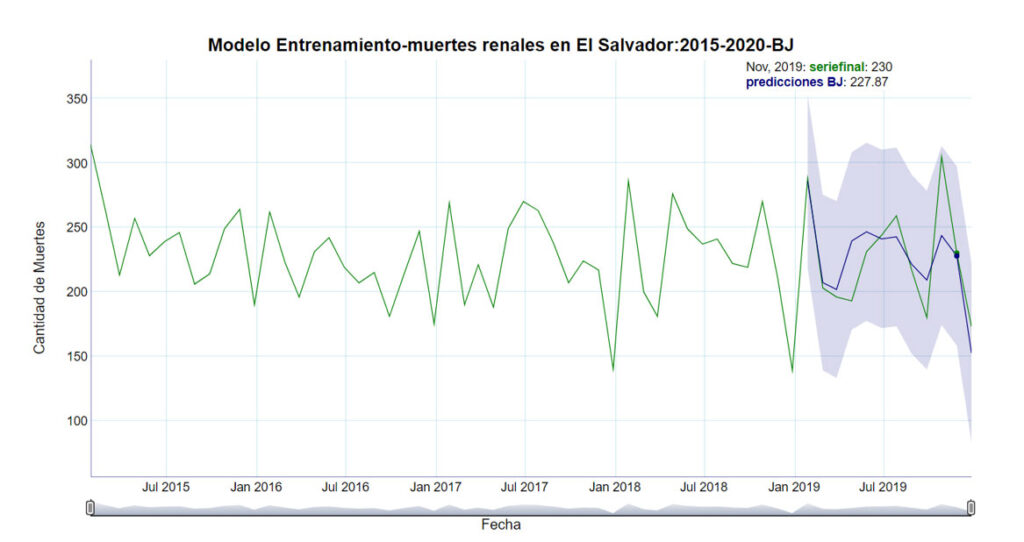
Para este modelo, con el método Box-Jenkins, se obtiene un error cuadrático medio de 25.48, lo cual evidencia que también es un excelente modelo para hacer las predicciones.
Se toma el modelo con el método Holt-Winters para realizar las predicciones del año 2020.
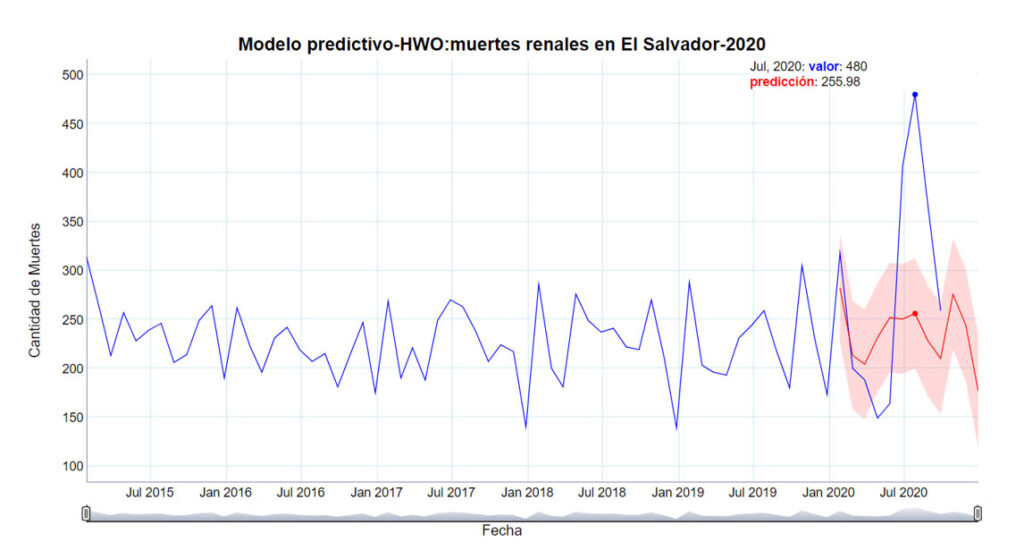
La figura cinco muestra las predicciones con dicho método y se comparan con los datos reales para dicho año, que se tienen hasta setiembre, el intervalo de confianza para las predicciones es de un nivel de confianza del 95%, por lo tanto, con una probabilidad del 0.95 los datos reales de dicho año deberían caer dentro de dicho intervalo.
Figura 5.
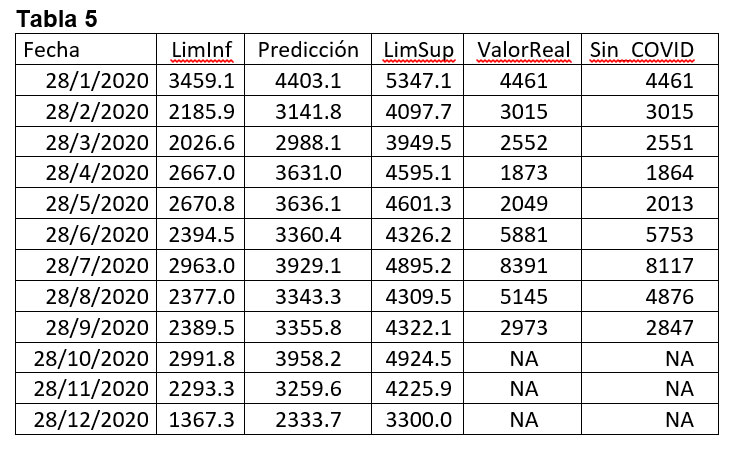
La tabla uno presenta las predicciones, el intervalo de confianza y los valores reales que se tienen para el año 2020. A la derecha están los parámetros del modelo ajustado.
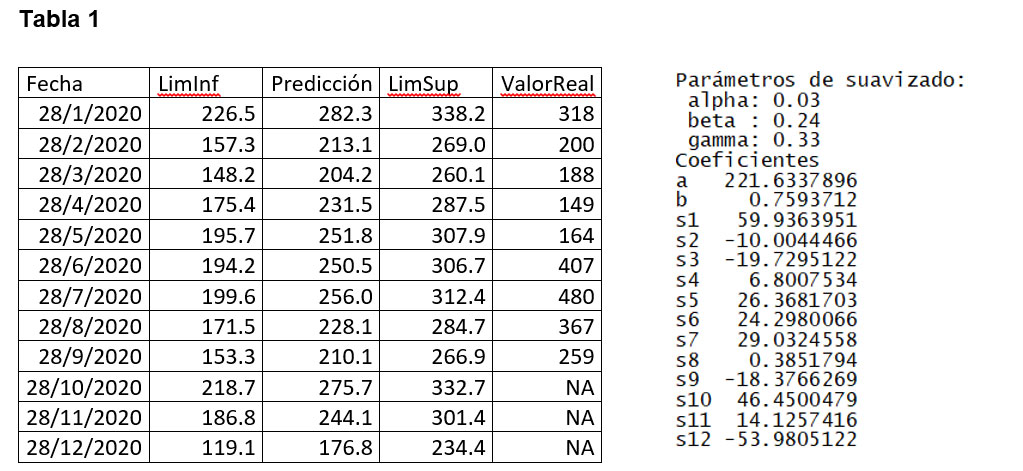
Los meses de abril, mayo, junio, julio y agosto caen fuera del intervalo de confianza. Para el mes de abril, el valor real tiene un porcentaje de decremento del 15% respecto al extremo inferior del modelo, para el mes de mayo, el valor real tiene un decremento del 16% respecto al extremo inferior del pronóstico.
Para el mes de junio, el valor real tiene un incremento del 33% respecto al extremo superior del valor pronosticado, en el mes de julio, el valor real tiene un incremento del 54%, respecto al extremo superior del valor pronosticado y este incremento es del 87% respecto al valor pronosticado según el modelo. Para el mes de agosto, el valor real experimenta un incremento del 29% respecto del extremo superior del valor pronosticado.
Todos los incrementos y decrementos anteriores tienen apenas una probabilidad del 5% de suceder, según el modelo ajustado, por lo tanto, son estadísticamente muy poco probables.
Análisis de muertes por cualquier tipo de paro
De las bases de datos de los años considerados se extraen todos los casos de muertes cuya causa común sea algún tipo de paro: cardiaco, respiratorio, cardiorrespiratorio. Se construye la serie mensual desde enero de 2015 hasta septiembre de 2020.
La figura seis muestra la evolución de muertes por paros, desde enero de 2015 hasta septiembre de 2020.
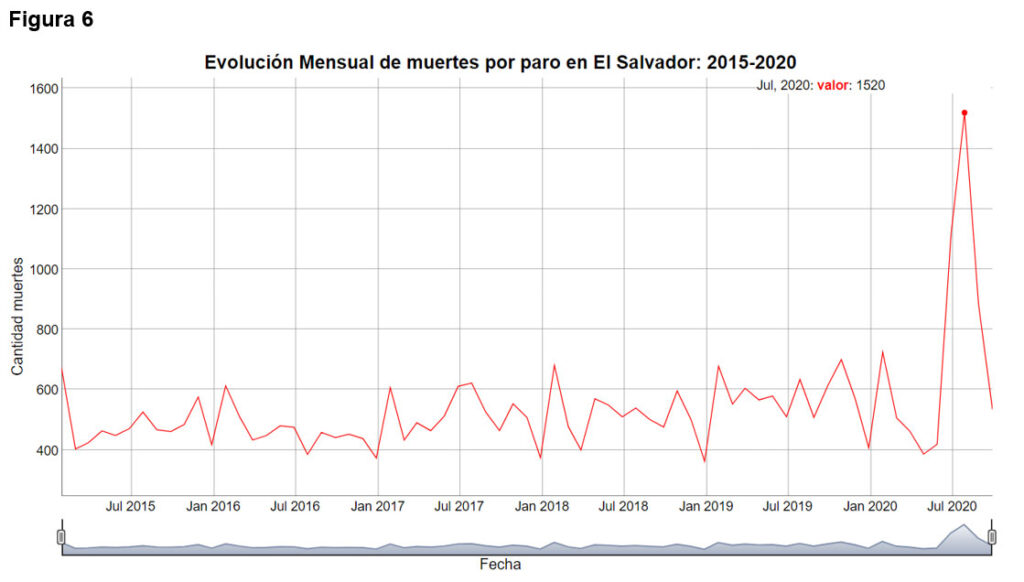
Los datos desde 2015 hasta 2018 cumplen el test de K-S, también desde 2015 hasta 2019 (p-valor de 0.85 y 0.88, respectivamente). Cuando se toman hasta septiembre de 2020 el p-valor baja hasta 0.17. En todos los casos, los datos cumplen dicho test y se prestan para ser predecibles a través de modelos de series de tiempo, lo cual permite predecir períodos a corto y mediano plazo, teniendo garantía que las predicciones serán robustas y altamente confiables.
La figura seis muestra la evolución de las muertes por algún tipo de paro, claramente se observa un cambio brusco de variabilidad en los datos correspondientes a los meses del año 2020.
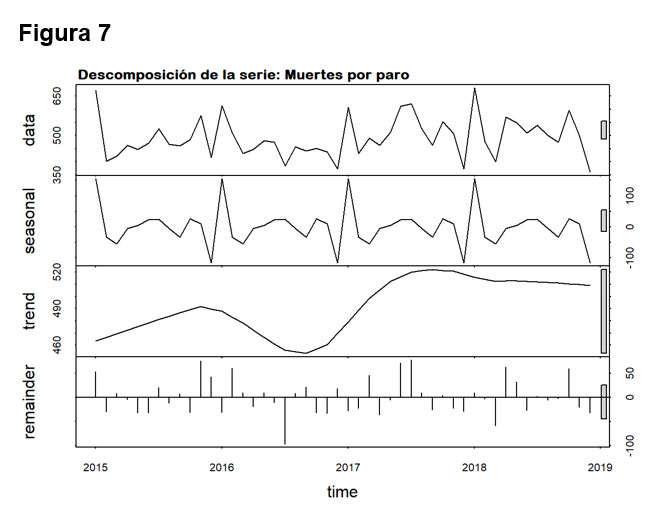
La figura siete muestra la descomposición de la serie, se observa que no tiene tendencia los primeros años, y luego se estabiliza, se identifica un componente estacional anual y normalidad de los residuos.
Se realizan las predicciones y junto a ellas un intervalo de confianza, con un nivel de confianza del 95%, por lo tanto, la probabilidad de que los datos reales estén en dicho intervalo de confianza es de 0.95.
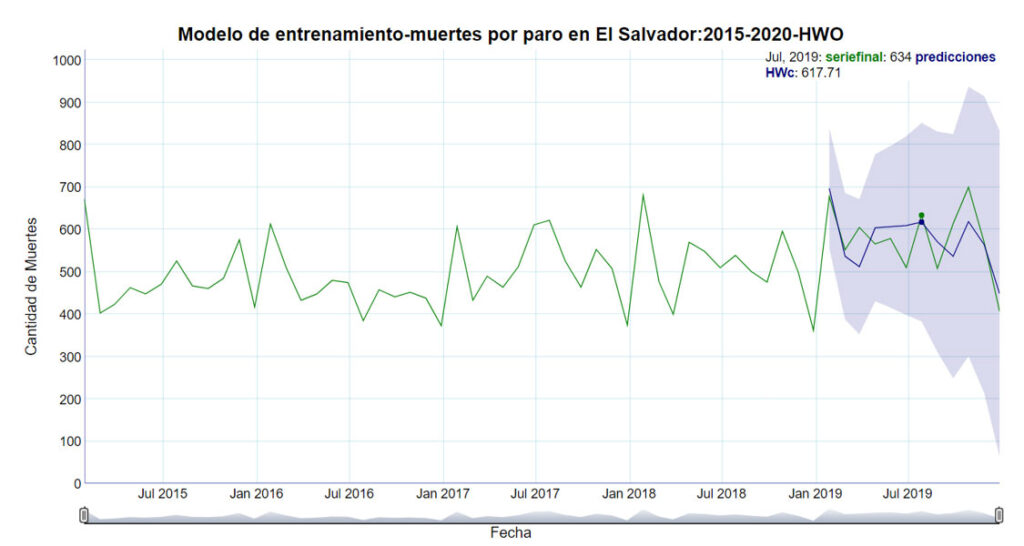
La figura ocho muestra el modelo de entrenamiento con el método Holt-Winters, optimizado a través de una heurística personal desarrollada. Como anteriormente se señaló, con dicho modelo se realizan las predicciones para el año 2019 y se prueba su bondad de ajuste con los datos reales de dicho año, se toman los parámetros que minimizan el error cuadrático medio (eso es lo que hace el algoritmo desarrollado). Como se puede observar a nivel gráfico, el ajuste de las predicciones es excelente y el intervalo de confianza generado sigue la tendencia de los datos reales, de acuerdo al periodo estacional anual de la serie. Para este modelo se obtiene un error cuadrático medio de 57.6
Figura 8
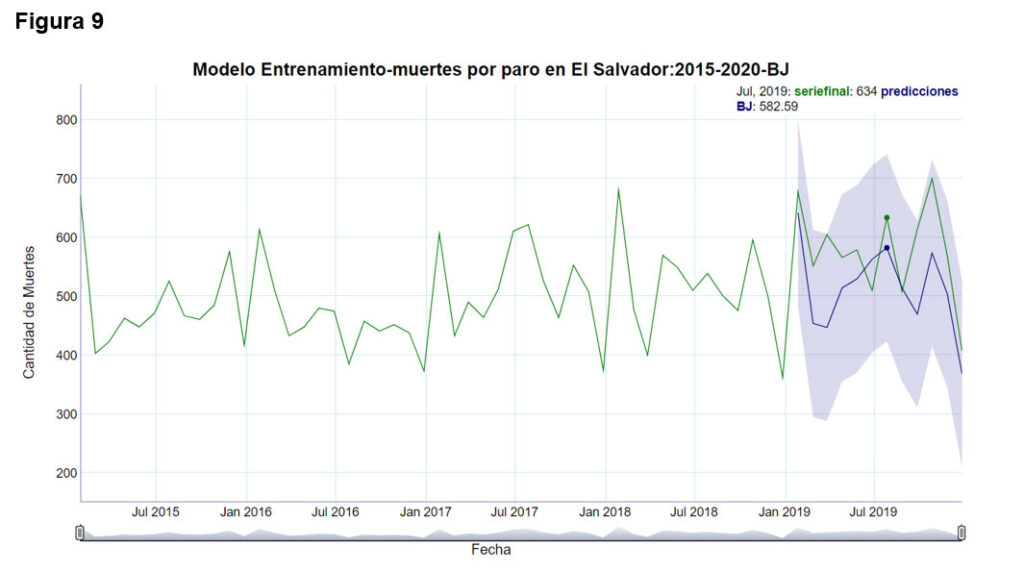
La figura 9 muestra el nivel de ajuste del modelo de entrenamiento, utilizando el método de Box-Jenkins, el cual supone un modelo SARIMA (0,0,0)(1,1,0)[12]. Se obtiene un error cuadrático medio de 86.09, lo cual evidencia que también es un excelente modelo para hacer las predicciones.
Se toma el modelo con el método Holt-Winters para realizar las predicciones del año 2020.
La figura diez muestra las predicciones con dicho método y se comparan con los datos reales para dicho año, que se tienen hasta septiembre, el intervalo de confianza para las predicciones es de un nivel de confianza del 95%, por lo tanto, con una probabilidad del 0.95 los datos reales de dicho año deberían caer dentro de dicho intervalo.
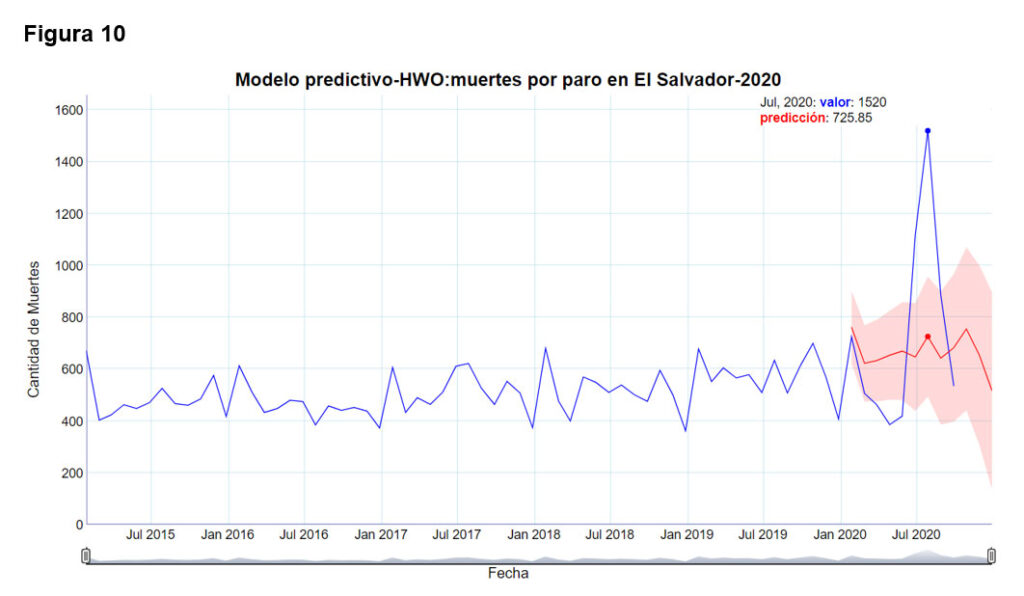
La tabla dos presenta las predicciones, el intervalo de confianza y los valores reales que se tienen para el año 2020. A la derecha están los parámetros del modelo ajustado.
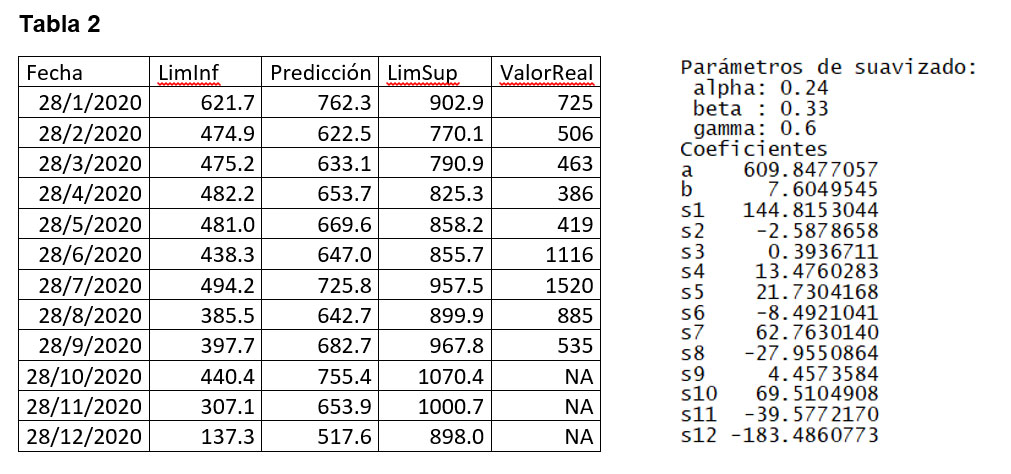
Los meses de marzo, abril, mayo, junio y julio, caen fuera del intervalo de confianza. Para el mes de marzo, el valor real tiene un porcentaje de decremento del 2.5% respecto al extremo inferior del modelo, para el mes de abril, el valor real tiene un porcentaje de decremento del 23.6% respecto al extremo inferior del modelo, para el mes de mayo, el valor real tiene un decremento del 13% respecto al extremo inferior del pronóstico.
Para el mes de junio, el valor real tiene un incremento del 30% respecto al extremo superior del valor pronosticado y en el mes de julio, el valor real tiene un incremento del 59%, respecto al extremo superior del valor pronosticado y este incremento es del 109% respecto al valor pronosticado según el modelo.
Tos los anteriores incrementos y decrementos, tienen apenas una probabilidad del 5% de suceder, según el modelo ajustado, por lo tanto, son estadísticamente muy poco probables.
Análisis de muertes por causa de cáncer
De las bases de datos de los años considerados, se extraen todos los casos de muertes cuya causa sea por cáncer y se construye la serie mensual desde enero de 2015 hasta septiembre de 2020.
Los datos desde 2015 hasta 2018 cumplen el test de K-S, también desde 2015 hasta 2019 (p-valor de 0.87 y 0.83, respectivamente). Cuando se toman hasta septiembre de 2020 el p-valor baja hasta 0.6. En todos los casos los datos cumplen para ser predecibles a través de modelos de series de tiempo.
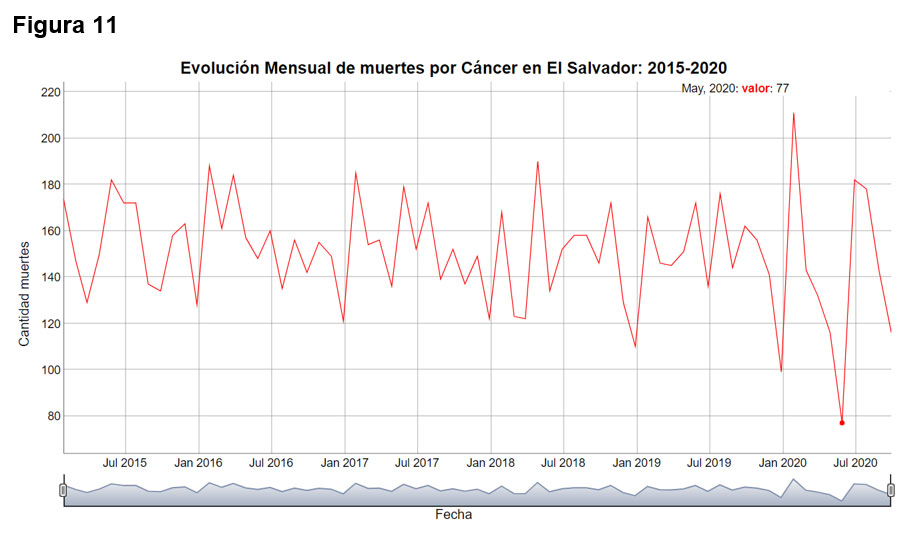
La figura 11 muestra la evolución de las muertes por cáncer notando un cambio brusco en la variabilidad de los datos de los meses del año 2020.
La figura 12 muestra el modelo de entrenamiento ajustado por el método de Holt-Winters, tal como se ha descrito anteriormente, optimizado por la heurística desarrollada, para el cual se obtiene un error cuadrático medio de 13.2, lo cual demuestra que tiene una alta capacidad predictiva.
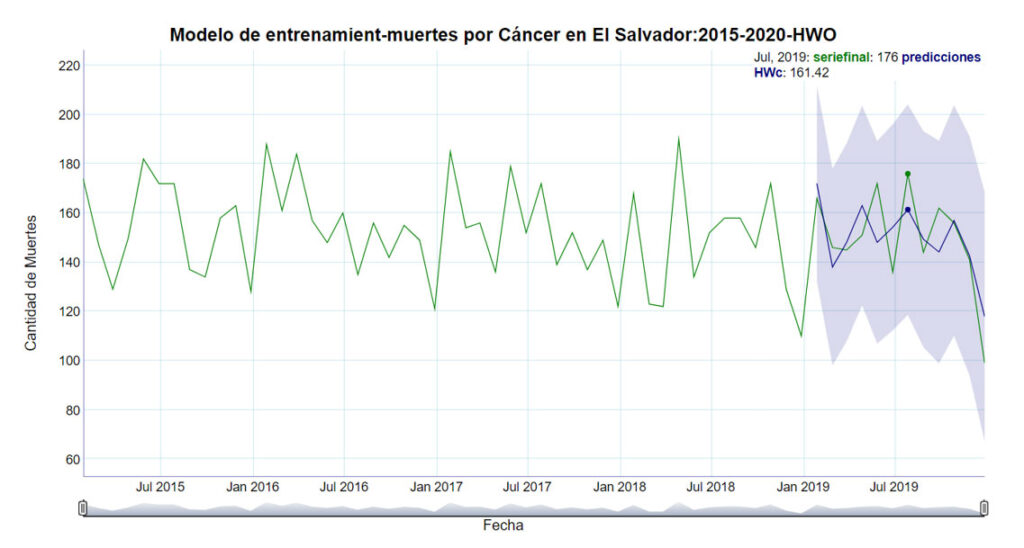
Se ve de manera gráfica el excelente ajuste del modelo de entrenamiento, los casos reales del año 2019 quedan todos dentro de los intervalos de confianza del modelo.
La figura 13 evidencia el modelo predictivo para el año 2020, utilizando el modelo de Holt-Winters optimizado, en la que se evidencia que para los meses de abril y mayo los valores reales caen fuera de los intervalos de confianza del modelo.
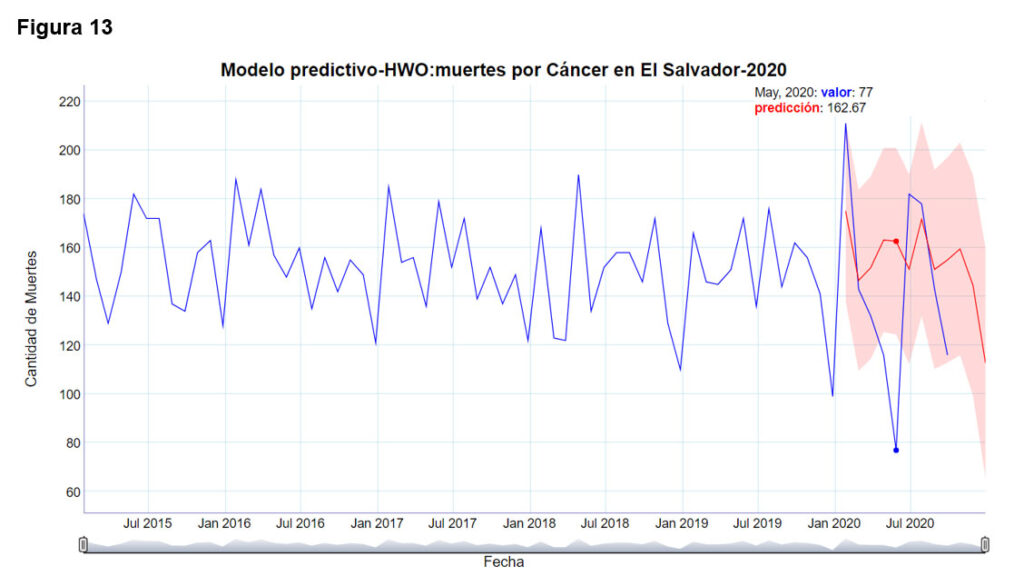
La tabla tres presenta las predicciones, el intervalo de confianza y los valores reales que se tienen para el año 2020. A la derecha están los parámetros del modelo ajustado.
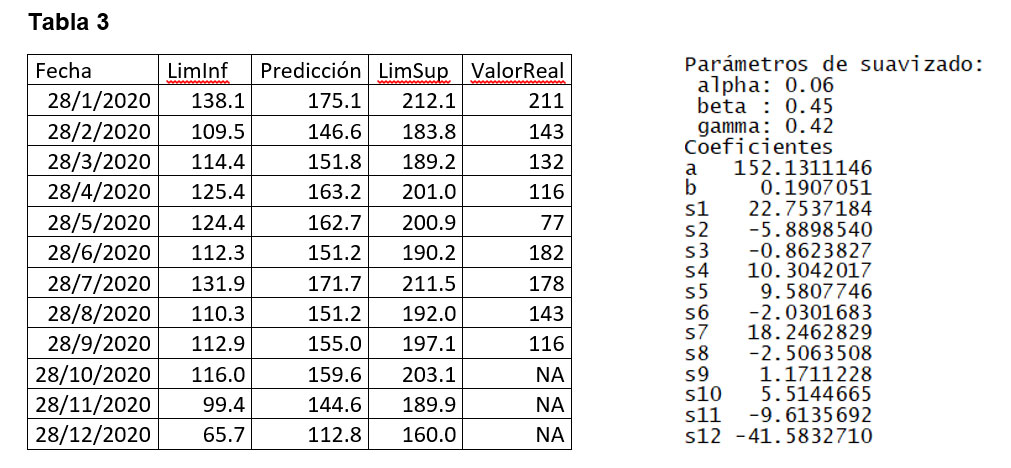
Los meses de abril y mayo caen fuera del intervalo de confianza. Para el mes de abril, el valor real tiene un porcentaje de decremento del 7.5% respecto al extremo inferior del modelo, para el mes de mayo, el valor real tiene un porcentaje de decremento del 38% respecto al extremo inferior del modelo.
Tos los anteriores decrementos, tienen apenas una probabilidad del 5% de suceder, según el modelo ajustado, por lo tanto, son estadísticamente muy poco probables.
Muertes naturales y por enfermedades en El Salvador - Periodo 2015-2020
Se analiza la evolución de muertes en El Salvador, sin contar las muertes por arma de fuego y accidentes de tránsito, las cuales consideramos son variables que han sufrido intervención en el año 2020, por lo tanto, se han eliminado todos los datos de muertes por estas causas, de todas las bases de datos consideradas (desde 2015 hasta 2020).
La figura 14 muestra la evolución de muertes por cualquier causa, excepto por armas de fuego y/o accidentes de tránsito. Se han pintado los datos por COVID-19 para los meses del año 2020. Claramente se observa un cambio brusco de variabilidad en los datos correspondientes a los meses del año 2020, y sobre todo no se evidencia una diferencia considerable al restar los datos por COVID-19 de cada mes.
Figura 14
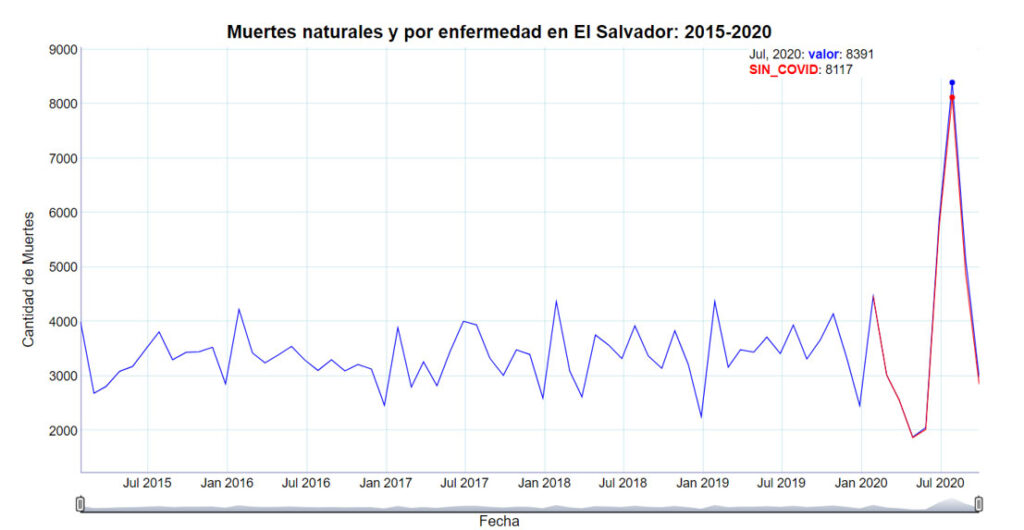
Los datos desde 2015 hasta 2018 cumplen el test de Kolmogorov-Smirnov, también desde 2015 hasta 2019 (p-valor de 0.84 y 0.87, respectivamente). Cuando se toman hasta septiembre de 2020 el p-valor baja hasta 0.16. En todos los casos los datos cumplen para ser predecibles a través de modelos de series de tiempo.
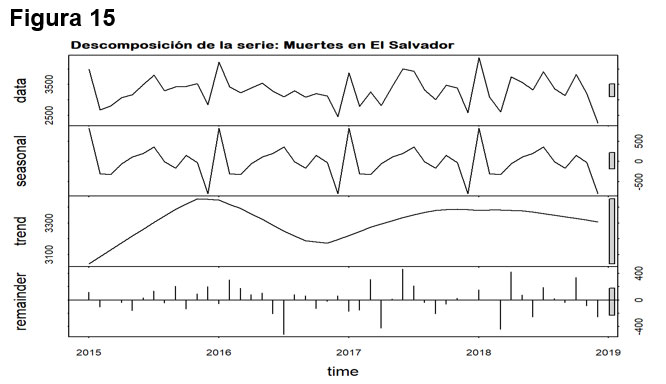
La figura 15, muestra la descomposición de la serie, se observa que no tiene tendencia los primeros años, y luego se estabiliza, se identifica una componente estacional anual y normalidad de los residuos.
Se realizan las predicciones y junto a ellas un intervalo de confianza con un nivel de confianza del 95%, por lo tanto, la probabilidad de que los datos reales estén en dicho intervalo de confianza es de 0.95.
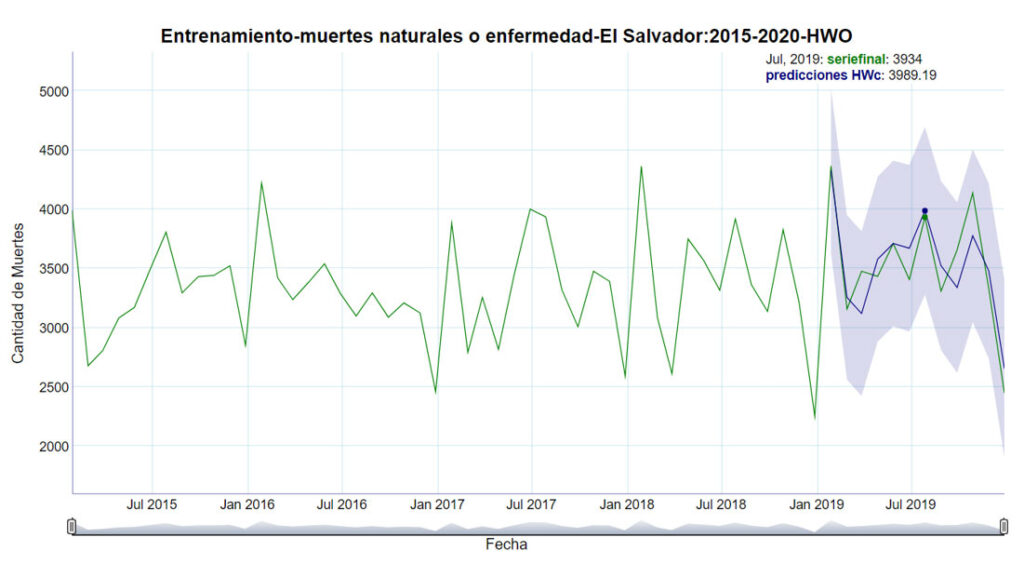
La figura 16, muestra el modelo de entrenamiento con el método Holt-Winters, optimizado a través de una heurística personal desarrollada. Como anteriormente se señaló, con dicho modelo se realizan las predicciones para el año 2019 y se prueba su bondad de ajuste con los datos reales de dicho año, se toman los parámetros que minimizan el error cuadrático medio (eso es lo que hace el algoritmo desarrollado). Como se puede observar a nivel gráfico, el ajuste de las predicciones es excelente y el intervalo de confianza generado, sigue la tendencia de los datos reales, de acuerdo al periodo estacional anual de la serie. Para este modelo se obtiene un error cuadrático medio de 219.1.
Figura 16
La figura 15, muestra la descomposición de la serie, se observa que no tiene tendencia los primeros años, y luego se estabiliza, se identifica una componente estacional anual y normalidad de los residuos.
Se realizan las predicciones y junto a ellas un intervalo de confianza con un nivel de confianza del 95%, por lo tanto, la probabilidad de que los datos reales estén en dicho intervalo de confianza es de 0.95.
La figura 16, muestra el modelo de entrenamiento con el método Holt-Winters, optimizado a través de una heurística personal desarrollada. Como anteriormente se señaló, con dicho modelo se realizan las predicciones para el año 2019 y se prueba su bondad de ajuste con los datos reales de dicho año, se toman los parámetros que minimizan el error cuadrático medio (eso es lo que hace el algoritmo desarrollado). Como se puede observar a nivel gráfico, el ajuste de las predicciones es excelente y el intervalo de confianza generado, sigue la tendencia de los datos reales, de acuerdo al periodo estacional anual de la serie. Para este modelo se obtiene un error cuadrático medio de 219.1
Figura 16
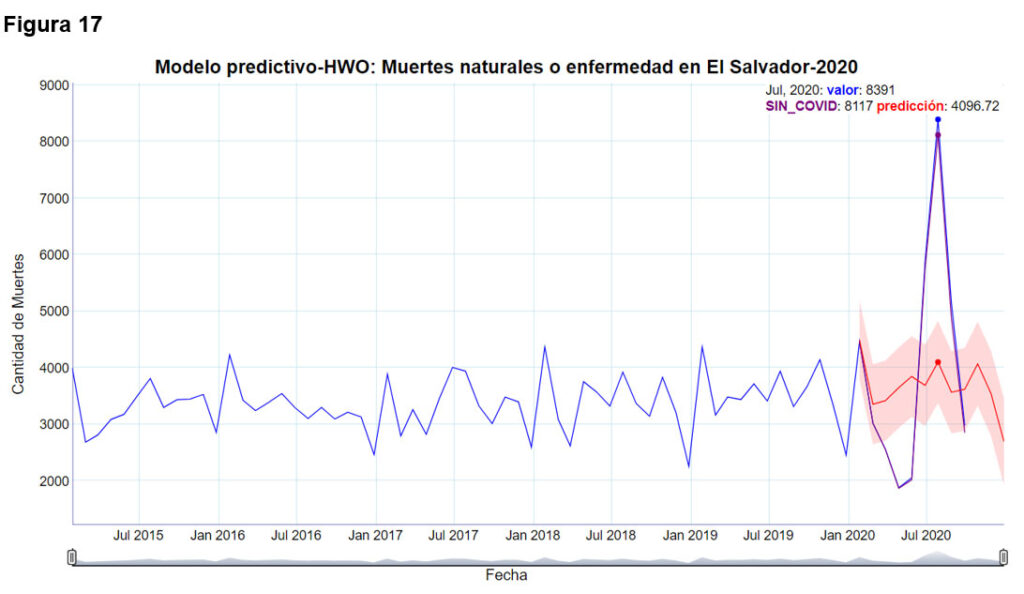
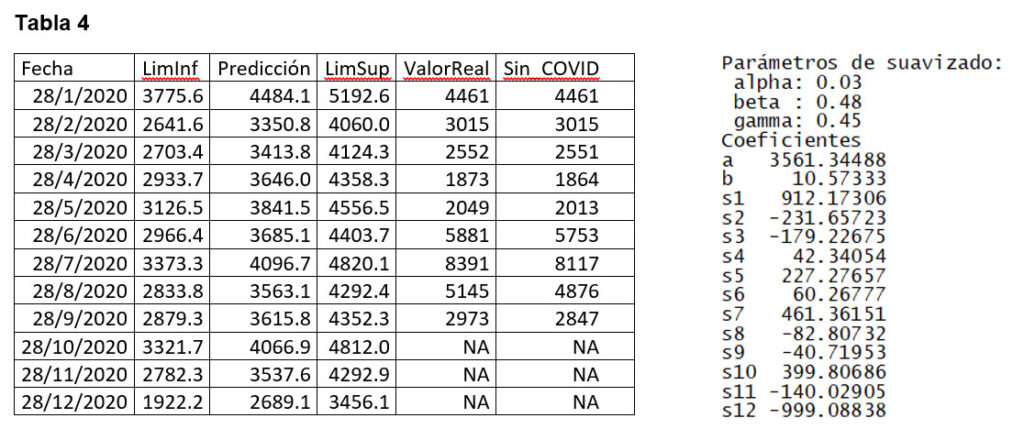
Los meses de marzo, abril, mayo, junio, julio y agosto caen fuera del intervalo de confianza. Para el mes de marzo, el valor real tiene un porcentaje de decremento del 5.6% respecto al extremo inferior del modelo, para el mes de abril, el valor real tiene un porcentaje de decremento del 36% respecto al extremo inferior del modelo, para el mes de mayo, el valor real tiene un decremento del 34% respecto al extremo inferior del pronóstico.
Para el mes de junio, el valor real tiene un incremento del 33.5% respecto al extremo superior del valor pronosticado y en el mes de julio, el valor real tiene un incremento del 74%, respecto al extremo superior del valor pronosticado y este incremento es del 104% respecto al valor pronosticado según el modelo. Si se compara con los datos mensuales sin COVID19, para julio se tiene un incremento del 68% respecto del extremo superior del pronóstico y es del 98% respecto del valor pronosticado.
Todos los incrementos y decrementos anteriores, tienen apenas una probabilidad del 3% de suceder, según el modelo ajustado, por lo tanto, son estadísticamente muy poco probables.
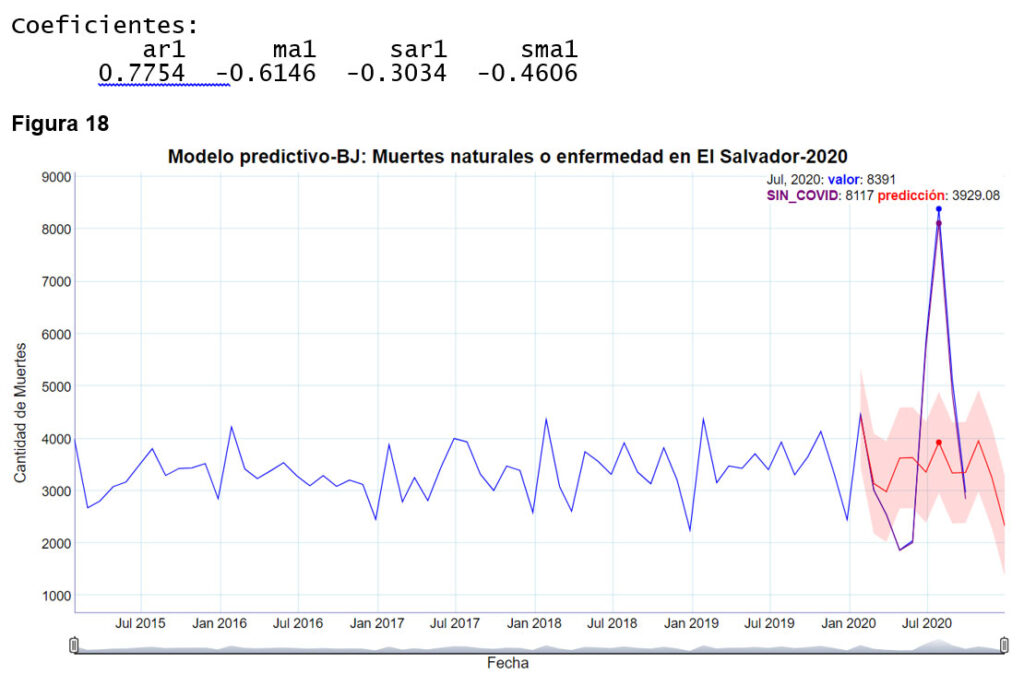
Se presentan en la Figura 18 y la Tabla 5 los resultados obtenidos ajustando un modelo SARIMA (1,0,1)(1,1,0)[12], con los siguientes parámetros:
Muertes totales en El Salvador-Periodo 2015-2020
Se analiza la evolución de muertes totales (todas las causas) en El Salvador.
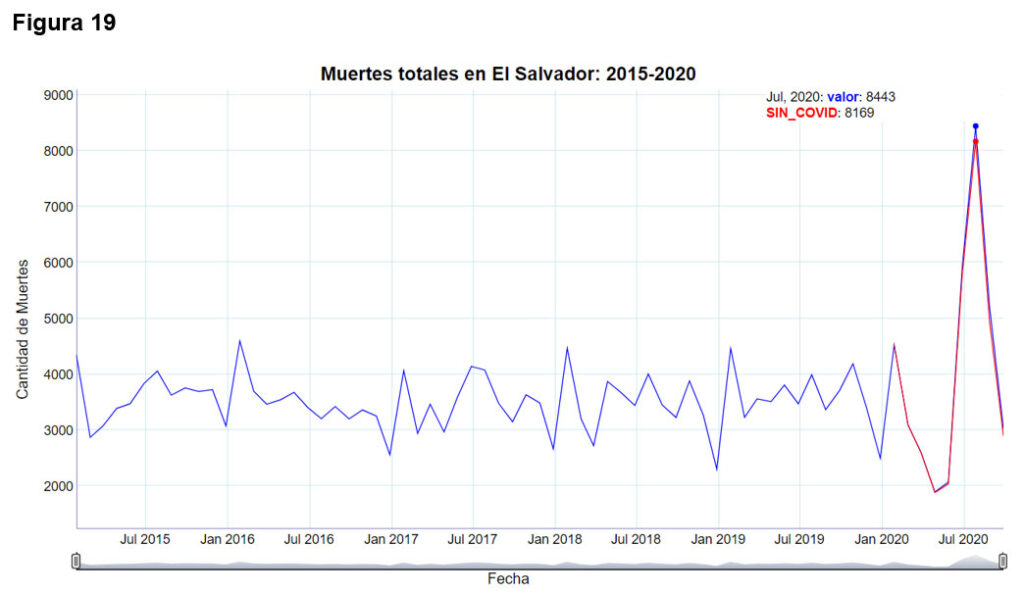
La Figura 19 muestra la evolución de muertes por cualquier causa, desde enero de 2015 hasta septiembre de 2020, además, se han pintado los datos totales menos las muertes debidas al COVID19, para los meses de enero a septiembre. Claramente se observa un cambio brusco de variabilidad en los datos correspondientes a los meses del año 2020, además, se evidencia que las muertes debidas al COVID19, no son las causantes del incremento/decremento brusco y estadísticamente no sostenible, que ha sucedido en los meses del año 2020.
Los datos desde 2015 hasta 2018 cumplen el test de K-S, también desde 2015 hasta 2019 (p-valor de 0.75 y 0.7, respectivamente). Cuando se toman hasta septiembre de 2020 el p-valor baja hasta 0.11 En todos los casos los datos cumplen para ser predecibles a través de modelos de series de tiempo.
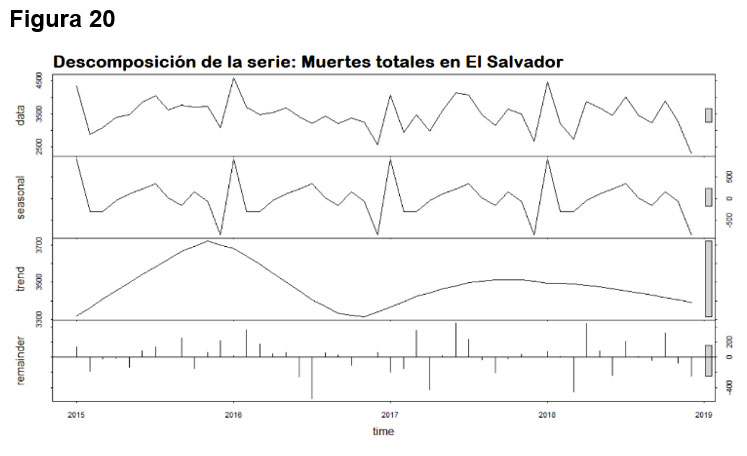
La figura 20 muestra la descomposición de la serie, se observa que no tiene tendencia los primeros años, y luego se estabiliza, se identifica una componente estacional anual y normalidad de los residuos.
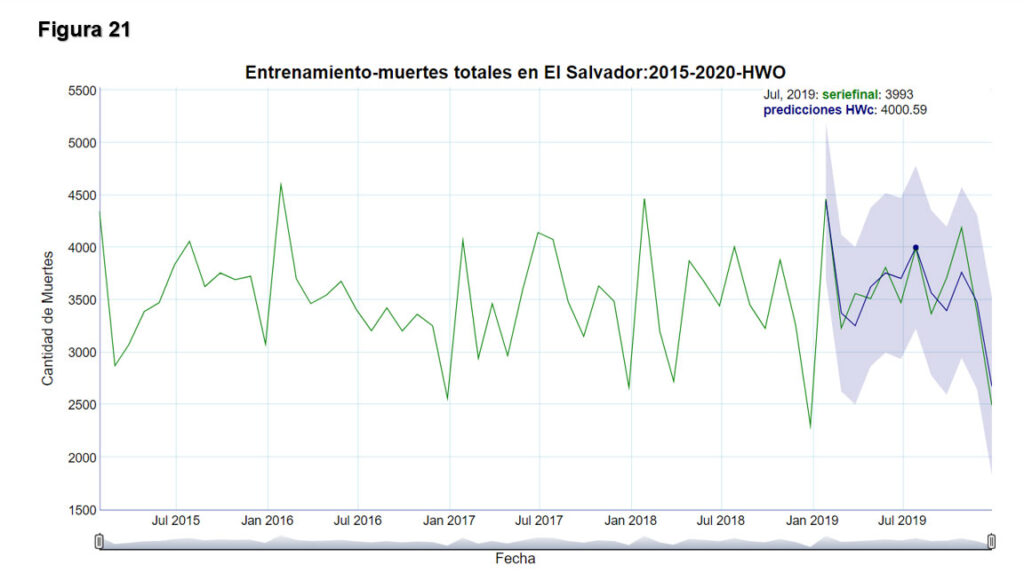
La figura 21 muestra el modelo de entrenamiento con el método Holt-Winters optimizado. Como anteriormente se señaló, con dicho modelo se realizan las predicciones para el año 2019 y se prueba su bondad de ajuste con los datos reales de dicho año, se toman los parámetros que minimizan el error cuadrático medio (eso es lo que hace el algoritmo desarrollado). Como se puede observar a nivel gráfico, el ajuste de las predicciones es excelente y el intervalo de confianza generado sigue la tendencia de los datos reales, de acuerdo al periodo estacional anual de la serie. Para este modelo se obtiene un error cuadrático medio de 213.4.
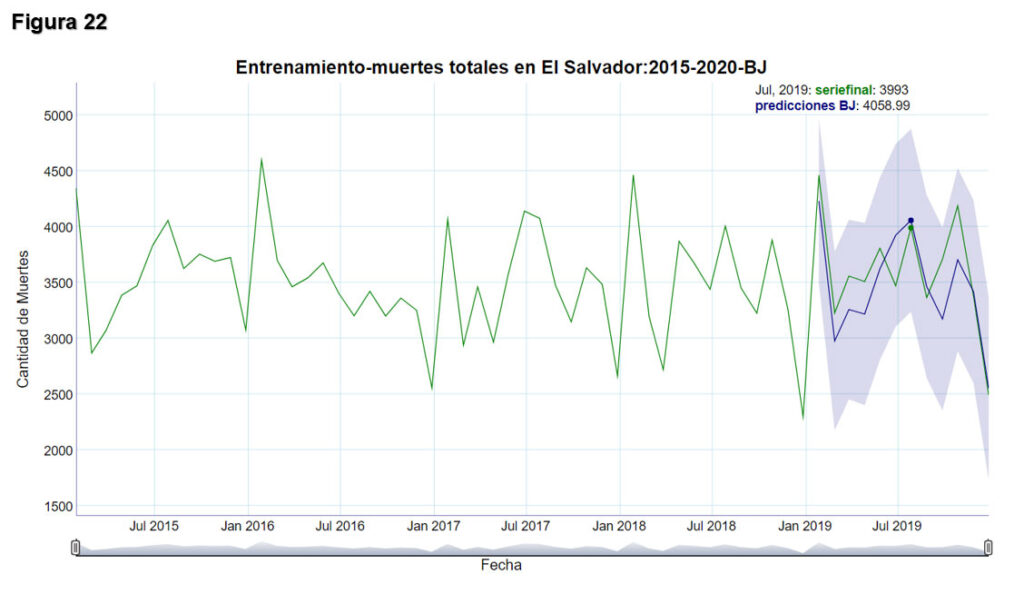
La figura 22 muestra gráficamente el nivel de ajuste del modelo con el método Box-Jenkins, donde se ha ajustado un modelo SARIMA (2,0,2)(1,1,0)[12]. Claramente se tiene un buen ajuste, pues el error cuadrático medio con este método es de 298.5.
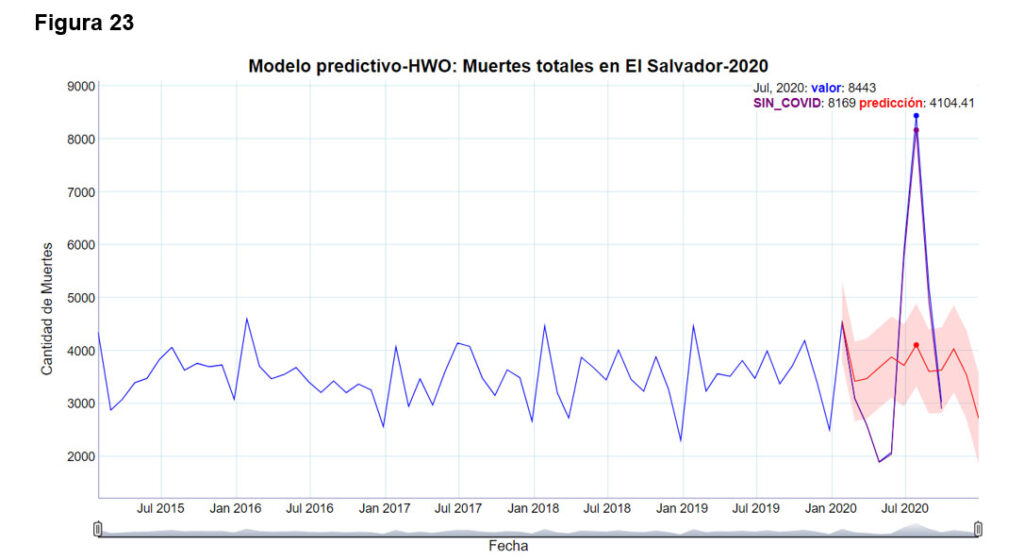
La figura 23 evidencia el modelo predictivo para el año 2020, utilizando el modelo optimizado con el método Holt-Winters, en la que se evidencia que para los meses de marzo, abril, mayo, junio, julio y agosto los valores reales caen fuera de los intervalos de confianza del modelo, que tienen un nivel de confianza del 97%, es decir con una probabilidad de 0.97 los valores reales deben caer dentro de tales intervalos de confianza.
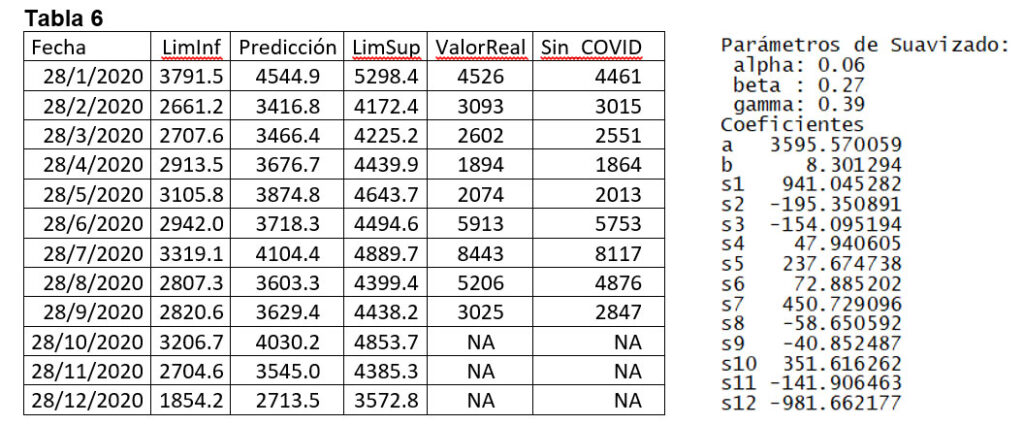
La tabla 6 muestra las predicciones para los meses del año 2020, junto con el intervalo de confianza generado, están los valores reales de dichos meses y los valores restando los casos de muerte por
COVID19 de cada mes, a la derecha los parámetros del modelo ajustado. Para el mes de marzo se
tiene un decremento del 3.9%, respecto al límite inferior del valor pronosticado, para el mes de abril se tiene un decremento del 35% respecto al extremo inferior del valor pronosticado, para el mes de mayo se tiene un decremento del 33% respecto al extremo inferior del valor pronosticado.
Para el mes de junio se tiene un incremento del 31.5% respecto al extremo superior del valor pronosticado, mientras que el incremento es del 59% respecto al valor pronosticado, para el mes de julio el in cremento es del 72.6% respecto del extremo superior del valor pronosticado, mientras que, respecto al valor pronosticado, el incremento es del 105.7%, para el mes de agosto el incremento respecto al extremo superior del valor pronosticado es del 18.3%, mientras que respecto al valor pronosticado el incremento es del 44.5%.
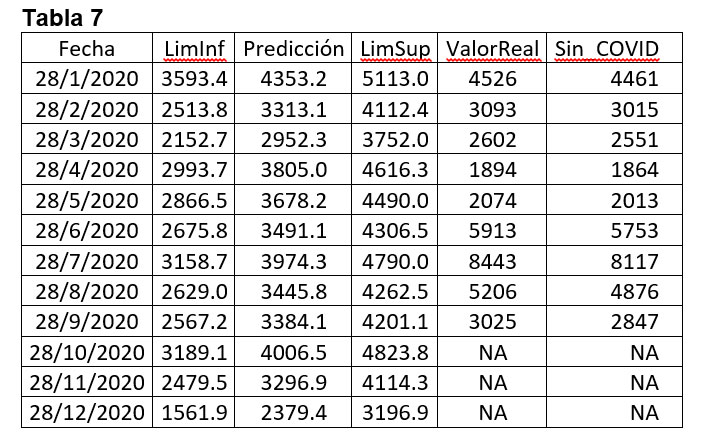
Para los datos reales restando los casos de COVID19 de cada mes, se tiene que el decremento para el mes de abril es del 36% respecto al extremo inferior del valor pronosticado, para el mes de mayo dicho decremento es del 35% respecto al límite inferior del valor pronosticado, para el mes de junio el incremento es del 28% respecto al límite superior del valor pronosticado y es del 55% respecto al valor pronosticado, para el mes de julio el incremento es del 66% respecto del extremo superior del valor pronosticado, y es del 97.8% respecto del valor pronosticado, para el mes de agosto el incremento es del 11% respecto al límite superior del valor pronosticado y es del 35% respecto del valor pronosticado.
Por todo lo anterior, el subregistro de muertes por COVID19 para el mes de junio puede llegar a ser hasta de un 55% y no menos de un 28%, análogamente, para el mes de julio el subregistro de muertes por COVID19 puede llegar a ser hasta de un 97.8% y no menos de un 66%, finalmente para el mes de agosto, el subregistro puede llegar a ser hasta de un 35% y no menos de un 11%, todo esto con una probabilidad muy alta de 0.97.
Sería muy importante tener los registros para los meses restante del año 2020, ya que de esta manera se puede tener una estimación altamente probable de dicho subregistro.
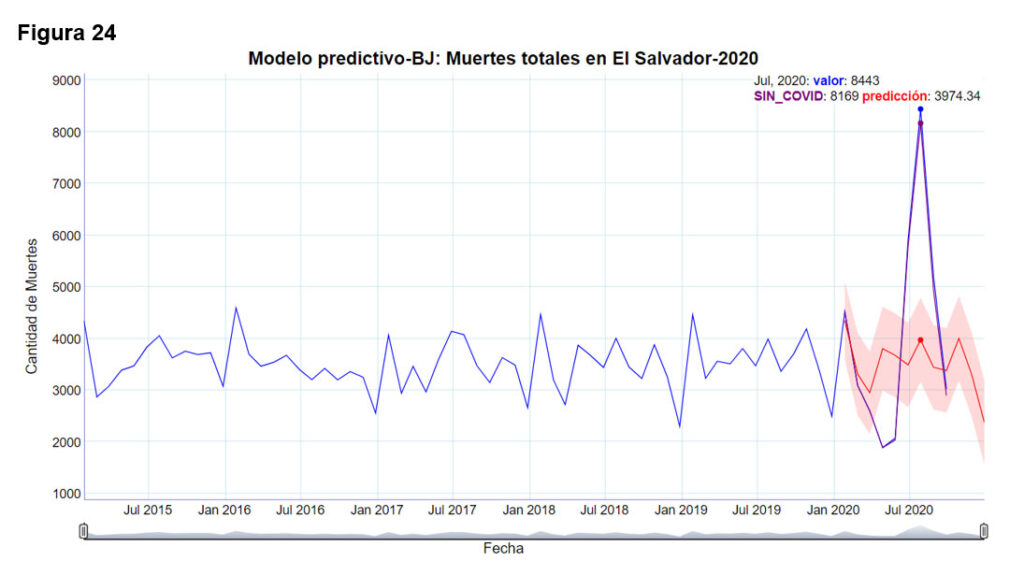
La figura 24 muestra el modelo ajustado con el método Box-Jenkins, SARIMA(2,0,2)(1,1,0)[12],
Coeficientes:
ar1 ar2 ma1 ma2 sar1
-0.0976 0.5412 0.4458 -0.5540 -0.6411
En este caso el dato real del mes de marzo, si cae dentro de los intervalos de confianza pronosticados, sin embargo, abril, mayo, junio, julio y agosto, caen fuera de la banda de confianza, la cual tiene un 97% de nivel de confianza.
En las figuras 23 y 24, se ha pintado la serie de casos de muertes, restando en cada mes, los casos debidos a COVID19. Como puede observarse, a pesar de restar los casos debidos a COVID19, el incremento para los meses de junio, julio y agosto sigue siendo muy alto.
La tabla siete muestra el pronóstico y un intervalo de confianza del 97% de nivel de confianza, para el modelo con el método Box-Jenkins.