Simulación: Modelo espaciotemporal / Cómo se movería el COVID19 por los municipios de El Salvador

Introducción 

El COVID-19 es un virus extremadamente contagioso. El número promedio de personas que puede contagiar un individuo infectado es calculado con el número reproductivo básico (𝑹𝟎) y se estima que el R0 para el coronavirus se encuentra entre 1.4 y cuatro personas contagiadas (Qun Li, 2020). En comparación con el de la influenza que es entre dos y tres (CE, JM, & M, 2004). Si este promedio es superior a uno, el número de casos crecerá exponencialmente dando lugar a una epidemia. Si es inferior a uno, la enfermedad eventualmente desaparecerá, ya que un infectado no alcanzará a infectar a más de un individuo. 

Para estas simulaciones, se utilizará el modelo compartimental SIR, desarrollado por Kermack y McKendrick. Este es un modelo simple en el que se toman en cuenta tres subpoblaciones:  

• Susceptibles (S): individuos sin inmunidad a la enfermedad. Estos son susceptibles a ser infectados.  

• Infectados (I): Portadores del virus. Estos individuos presentan síntomas de la enfermedad, y pueden transmitirla al entrar en contacto con personas susceptibles.
   
• Recuperados (R): Personas que no pueden transmitir la enfermedad, ya que se recuperaron de la enfermedad, o murieron por causa de esta.  

Las personas se trasladan del compartimento S al compartimento I por la tasa de infección que representa la probabilidad que una persona susceptible sea contagiada al tener contacto con un infectado. Para pasar del compartimento I al compartimento R, los individuos tienen que recuperarse, por lo que tienen que superar el período infeccioso promedio. La probabilidad con la que los individuos se recuperan está dada por la fórmula:  

Supuestos 

Para el coronavirus, se utilizó un período infeccioso promedio de 25 días, por lo que la probabilidad de recuperación será 0.04. En cuanto a la tasa de infección, se calculó con el número reproductivo básico, de fórmula para el modelo clásico SIR:  

 Para propósitos demostrativos, se consideró una distribución probabilística Gamma de media igual a 3 y de forma 1.5. Se tomó como tasas de infección valores aleatorios siguiendo esta distribución para cada día de la simulación. Esto hará que el número reproductivo básico sea diferente para cada ubicación. 

Con respecto a la distribución de la población por municipios se tomaron los datos del último censo de población y vivienda del 2007, publicado en el sitio web de la Dirección General de Estadística y Censos. 

Lo característico de este modelo, es la utilización de una matriz de transporte (también llamada matriz de origen-destino) para graficar la transmisión de la enfermedad en diferentes puntos del país. Esta matriz representa el flujo de individuos que se movilizan de un lugar a otro. 

Para estimar dicha matriz, se utilizaron los datos disponibles sobre las rutas y paradas de autobuses en El Salvador, disponibles en el sitio web horariodebuses.com. 

Además, se tomó un coeficiente de movilidad urbana igual a 20 %, el cual representa la influencia del transporte colectivo con respecto al particular. 

Se escogió infectar en un principio el municipio, de cada departamento, con una mayor relación entre su población y su importancia en movilidad.  

Se toma como número de primeros infectados el 0.5 % de la población del municipio escogido, y se efectúa la simulación durante un período de 100 días a partir de la primera infección.  

Objetivo 

El propósito del simulador es servir como herramienta para analizar el impacto de ciertas medidas tomadas con el objetivo de minimizar la propagación del COVID-19. Así como observar cómo una red de conexiones puede servir para dar una idea de lo que sucede durante un brote epidémico en El Salvador. 

Se analizará cada caso según de la ubicación de las primeras infecciones.  

Análisis 

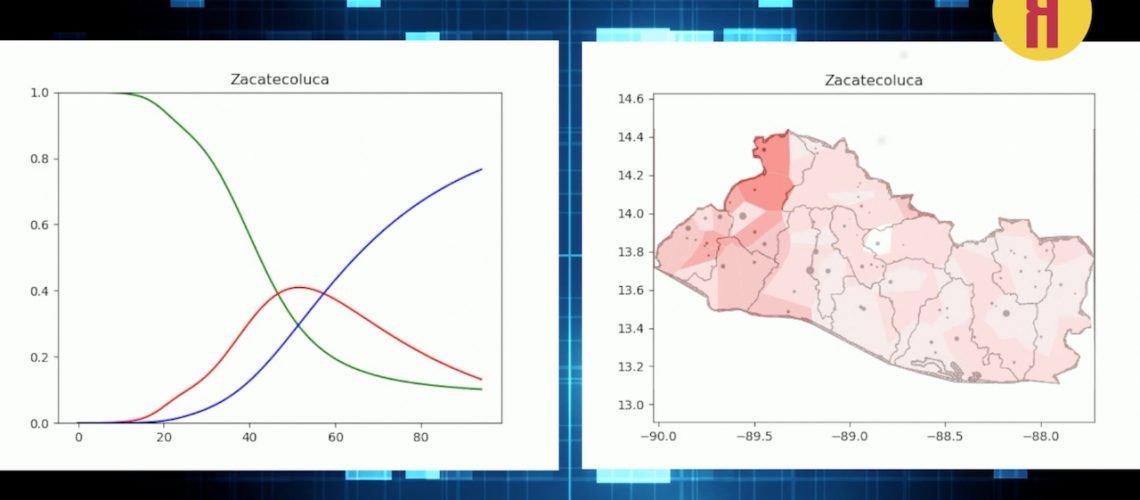
Cada punto presente en el mapa representa una parada de autobús. El tamaño de los puntos simboliza la cantidad de rutas que circulan en dicha parada. 

En cuanto al gráfico, el eje vertical representa la población en porcentaje, y el eje horizontal representa el tiempo en días.   

Existen casos, como cuando las primeras infecciones ocurren en Sonsonate, donde al final de la simulación quedan zonas en las cuales ocurrieron pocos casos de coronavirus.  

Como era esperado, se observa que en la mayoría de los casos los primeros lugares en infectarse son aquellos que tienen una alta relevancia en su población y en el número de rutas que los atraviesan.  

También se puede ver, por medio de los gráficos, que el pico de infectados se encuentra entre 0.4 y 0.6 para la mayoría de las simulaciones, y que este ocurre entre 30 y 60 días después de la primera infección.  

En algunos casos, la curva de infectados es inclinada, angosta y con un máximo relativamente elevado (San Miguel, Ahuachapán). Mientras que, en otros, la curva tiene una forma más plana, más larga y con un pico más bajo (San Salvador, La Libertad, Zacatecoluca).  

Esto se puede explicar puesto que en zonas con alta densidad poblacional o zonas con alta importancia en la movilidad, más personas se enferman y contagian a otras, por lo que la enfermedad estará presente durante un período más largo.  

Conclusiones 

Se puede concluir que la movilidad en el país, así como las fuertes concentraciones de personas, tiene un alto peso en cuanto a la transmisión de enfermedades infecciosas.  

Sin embargo, independientemente de donde comience la epidemia, siempre se obtienen resultados indeseables para el bien de los salvadoreños. Por lo que se recomienda evaluar la opción de acatar o tomar medidas para evitar, en lo posible, la propagación del COVID-19. 

Próximamente, se examinará el efecto de medidas de cuarentena en diferentes regiones del país, así como el impacto al disminuir el uso del transporte colectivo.